Представь: заказчик просит назвать дедлайн по проекту как можно скорее. Но есть нюанс: работать будут спецы, которых наняли буквально вчера, и ты понятия не имеешь, что из этого выйдет.
Вместо того чтобы ответить: «Как карта ляжет», можно воспользоваться методом Монте-Карло — получить вероятный результат, от которого уже можно отталкиваться.
Рассказываем, что это за метод, зачем он нужен проджектам, топ-менеджерам и вообще всем, чья сфера связана с неопределённостью, но при этом требует конкретных результатов.
Что такое метод Монте-Карло простыми словами
‼️ Дисклеймер: метод Монте-Карло — сложнейший в плане вычислений. В этой статье мы рассмотрим самые простые вариации. Но держи в уме, что их множество
— это способ решать сложные задачи с помощью случайных чисел
Допустим, тебе нужно срочно посчитать конкретный показатель чего-либо,
но формула слишком запутанная и ты не знаешь точного способа найти ответ. Вместо того чтобы ломать себе голову, можно 10 тысяч раз подставить случайные значения и посмотреть, какой результат получается чаще всего.
Суть метода Монте-Карло — заменить сложные вычисления множеством случайных экспериментов. Схема рабочая, потому что, когда мы делаем множество случайных попыток, средний результат становится близким к настоящему ответу. Чем больше таких попыток, тем точнее будет решение задачи
История возникновения
Метод Монте-Карло придумали физики, чтобы облегчить себе жизнь. Учёные Джон фон Нейман и Станислав Улам в первой половине XX века участвовали
в разработке ядерной бомбы в США.
Они искали способ смоделировать множество ядерных реакций в условиях неопределённости, чтобы в будущем использовать результаты для исследований.
Математика и физика хоть и точные науки, но в них много неизвестного. Иногда невозможно найти нужную формулу, чтобы вычислить точное значение переменной.
Для этого и используют метод Монте-Карло — чтобы получить примерные результаты и на их основе принимать решения.
Почему математический метод называют Монте-Карло
Потому что его результаты — это вероятность, как в любой азартной игре. Монте-Карло — район в Монако, куда съезжаются люди со всего мира поиграть в казино. Каждый раз игроки понятия не имеют, проиграют всё или станут сказочно богаты.
Принцип Монте-Карло похож на игру в рулетку: ты делаешь ставку на рандомное число, а пока крутится рулетка, у шарика есть бесконечное количество вариантов развития событий.
То же самое и в математических расчётах или в любой другой сфере, где неопределённость — это базовый минимум. Метод Монте-Карло помогает эти варианты увидеть, зафиксировать и сопоставить их с условиями задачи.
Но существует и немного другая версия, почему метод назвали именно так.
Области применения метода Монте-Карло
Можно предположить, что метод Монте-Карло применяется почти везде.
Но особенно — в следующих областях:
- Физика — для нейтронно-физических расчётов активных зон реакторов
- Экономика — посчитать курс валюты и сделать прогнозы ставок ЦБ
- IT — спроектировать сложные инженерные системы и анализировать их надёжность
- Бизнес — просчитать прибыль в условиях экономической нестабильности
- Логистика — построить самый оптимальный маршрут с учётом возможных пробок или перекрытий дорог
- Маркетинг — спрогнозировать продажи нового продукта на рынке
- Реклама — оценить, как пользователи будут взаимодействовать с рекламной кампанией
Для чего используют метод Монте-Карло в управлении проектами
С помощью метода Монте-Карло управленцы оценивают риски новых проектов или принимают важные решения по продукту в условиях тотальной неопределённости. Но это ещё не всё:
| Для чего нужен | Какой вопрос закрывает | Какие условия |
|---|---|---|
| Рассчитать сроки проекта | «Какова вероятность, что мы успеем сдать проект за два месяца?» | Ты не знаешь, сколько задач в день выполняют твои коллеги |
| Прикинуть бюджет | «Нам выделили миллион рублей. Мы на 100% уложимся в эту сумму? Нужно ли нам попросить ещё?» | Курс доллара и цены на всё меняются быстрее, чем ты успеваешь моргнуть |
| Спрогнозировать примерную прибыль | «Какова вероятность, что мой проект станет прибыльным?» | Ты не понимаешь, каким будет поведение пользователя |
Как работает метод Монте-Карло: принцип и алгоритм
Глобально метод Монте-Карло отвечает на один вопрос: «Какова вероятность такого-то события?» Например: «Успеет ли команда, которую только-только наняли в проект, закончить его за 20 дней?» Результат — это вероятность. Например, 90% или 10%
Метод основывается на двух вещах:
- Генерация тысяч (или сотен тысяч) случайных значений для всех неизвестных параметров задачи
- Анализ статистики — то есть всех полученных результатов, а это тысячи разных сценариев, при которых значения неизвестной величины всегда разные
Как генерируются значения в методе Монте-Карло
Случайные значения генерируются не с потолка, а на основе примерных данных, которые уже есть. Для этого нужно проанализировать предыдущие показатели
и выявить для себя три возможных сценария развития событий — это называется «Метод треугольника» 👇
| 🤩 Оптимистичный | 🙂 Наиболее вероятный | 😪 Пессимистичный |
|---|
В каждом варианте нужно указать диапазон значений. На них ориентируется программа, чтобы прогнать сотни или тысячи вариантов развития событий: чем больше — тем точнее будет результат.
На случай если у тебя нет вообще никакой информации, можно подобрать рандомные значения — для этого используют генератор случайных чисел.
Где строить вероятности по методу Монте-Карло: Excel (базовый уровень), Python и другие специализированные программы с огромными мощностями — подобными пользуются корпорации (например, Росатом) для собственных вычислений. Если данных и вероятностей сотни тысяч, то и оборудование должно соответствовать мощности.
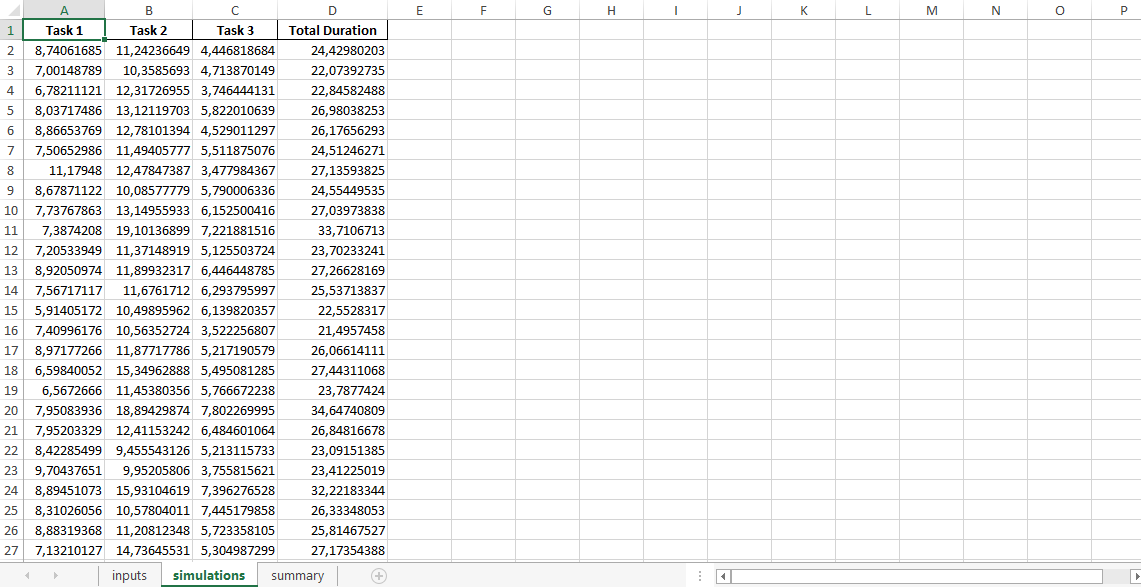
Результат метода Монте-Карло — огромная сводная таблица с километровыми столбиками со случайными значениями, которые нужно отсортировать по трём группам: оптимистичные, наиболее вероятные или пессимистичные.
Анализ результатов
На основе огромного массива данных можно построить график кумулятивного распределения — результаты ты увидишь на двух осях. Горизонтальная обозначает значения, а вертикальная — процент вероятности от самой низкой до самой высокой.
Построить график кумулятивного распределения можно с помощью нейросетей — достаточно загрузить табличку с данными и попросить ИИ её проанализировать
и составить график.
Метод не просто показывает тебе фиксированный результат, а указывает диапазон. Например, с вероятностью 80 % проект завершится между 20 и 25 днями.
Как найти вероятность по методу Монте-Карло
Дисклеймер: метод Монте-Карло используют в разных областях, в том числе и для сложнейших расчётов. Мы покажем упрощённый вариант
Да, чтобы посчитать вероятность по методу Монте-Карло, придётся напрячься.
Но если ты не собираешься вычислять вероятность взаимодействия нейтронов, то хватит базовых знаний и нашей небольшой памятки.
-
Определи задачу — чётко сформулируй, какую задачу надо решить
с помощью Монте-Карло. На этом этапе важно понять: нужен ли тебе этот метод вообще - Сгенерируй случайные числа или возьми предыдущие значения — используй генератор случайных чисел, чтобы создать множество разных вариантов (сценариев). Программа для каждого варианта выберет случайным образом значения для всех переменных
- Смоделируй вероятность — внеси все свои данные в программу для моделирования и запусти её. В основном для этого используют специальные формулы в Excel или коды — если строишь вероятность в Python. После система начнёт генерировать тысячи вариантов развития событий
-
Проанализируй результаты — собери все результаты, отсортируй их
и построй график кумулятивного распределения
Пример: как рассчитать сроки проекта с помощью метода Монте-Карло
Шаг 1: определяемся с задачей
Представь: нужно запустить новую фичу в мобильном приложении за 21 день. Задача — оценить, успеет ли команда уложиться в сроки.
Над фичей работают три разработчика, а проект состоит из трёх этапов:
- бэкенд (серверная часть)
- фронтенд (интерфейс)
- тестирование и правка багов
Ты не знаешь точно, сколько продлится каждый. Метод Монте-Карло поможет учесть эту неопределённость.
Шаг 2: генерируем значения
Загадай для каждого этапа не одно число, а три — по методу треугольника,
о котором рассказывали выше. Распредели эти значения как в табличке ниже.
| Этап | Оптимистичная | Наиб. вероятная | Пессимистичная |
|---|---|---|---|
| Бэкенд | 3 дня | 5 дней | 8 дней |
| Фронтенд | 4 дня | 6 дней | 10 дней |
| Тестирование | 2 дня | 4 дня | 7 дней |
Компьютер будет использовать эти данные, чтобы симулировать разные сценарии.
‼️Если между задачами есть зависимость, то её нужно указать. В противном случае программа посчитает всё неправильно, потому что не будет знать, что тестирование нельзя начать до того, как команда закроет предыдущие задачи
Шаг 3: моделируем вероятности
Компьютерная программа будет использовать данные из таблички выше
и ориентироваться на колонку с наиболее вероятными значениями. 10 тысяч раз она сделает следующее:
-
Для бэкенда случайным образом выберет длительность между 3 и 8 днями,
но так, чтобы значения ближе к 5 дням выпадали чаще - Для фронтенда выбирает длительность между 4 и 10 днями (чаще ~6 дней)
- Для тестирования выбирает длительность между 2 и 7 днями (чаще ~4 дня)
Далее суммирует три полученных числа. Это и есть длительность проекта в одной симуляции. Ниже — примеры 5 случайных симуляций.
| Попытка | Бэкенд | Фронтенд | Тестирование | Итого |
|---|---|---|---|---|
| 1 | 4 д. | 5 д. | 3 д. | 12 д. |
| 2 | 6 д. | 7 д. | 5 д. | 18 д. |
| 3 | 5 д. | 10 д. | 4 д. | 19 д. |
| 4 | 3 д. | 6 д. | 6 д. | 15 д. |
| 5 | 7 д. | 8 д. | 7 д. | 22 д. |
Шаг 3: анализируем результаты
Когда компьютер закончит прогонять 10 тысяч значений, ты всё равно не увидишь один чёткий ответ. На экране будет распределение вероятностей.
Допустим, результаты такие:
- Количество симуляций, где уложились в 21 день: 8500
- Общее количество симуляций: 10 000
Расчёт вероятности ⬇️
Вероятность = (8500 / 10 000) * 100 % = 85 %
Вероятность уложиться в 21 день — 85 % (это и есть наш ответ), а за 25 дней — почти 100 %.
Что с этими данными делать — решать тебе. Можно начать работу с тем, что есть, или накинуть сверху пять дней, чтобы назвать заказчику срок, за который команда точно справится.
Преимущества и недостатки метода
Монте-Карло упрощает жизнь, но есть условия, при которых он становится бесполезным. Поэтому перед тем, как открыть генератор случайных чисел, сверься с нашей табличкой ⬇️
| ✅ Да | ❌ Но |
|---|---|
| Метод хоть и не даёт точных результатов, но от них уже можно отталкиваться и принимать решения | Если изначальные значения были нереалистичными, то и результат будет таким же |
| Монте-Карло упрощает жизнь — не нужно искать дополнительные формулы для расчёта и ломать себе голову. Можно заменить неизвестные переменные случайными числами | Для наиболее точных результатов нужна мощная техника, время на анализ и знания программы, чтобы она работала правильно и выдавала адекватный результат |
| Здорово, что можно посчитать дедлайн по проекту в условиях дичайшей неопределённости | Если не указать в программе зависимости между задачами, то результаты будут неточными |
Часто задаваемые вопросы (FAQ)
Что ограничивает точность метода Монте-Карло?
Как мы уже выяснили, метод Монте-Карло — вещь полезная, но для того, чтобы она приносила реальные результаты, нужно учитывать ограничения:
- Итерации — это то, сколько раз система прогнала возможные вероятности. Если их будет меньше тысячи, то результат будет нереалистичным. Чем больше прогонов, тем точнее итоговые значения
- Распределения — это относится к методу треугольника. Если неправильно распределить итоговые значения, то результат сместится или исказится
- Зависимости — если не расставить их по задачам, то есть риск получить не тот результат
Какой результат Монте-Карло считается хорошим?
Тот, который максимально приближен к реальности и стабилен при повторных расчётах: если попросить систему выполнить те же действия, то ничего не изменится. То же самое должно произойти, если увеличить количество итераций — например с 10 тысяч до 100 тысяч.
Коротко о главном
- Метод Монте-Карло используют, когда есть задача с неизвестными переменными. Вместо того чтобы искать нужную формулу, можно заменить данные случайными числами и посчитать вероятность — это и будет решение задачи
-
В управлении проектами метод используют, чтобы просчитать риски
по проекту, бюджет и сроки в условиях неопределённости - Результат метода Монте-Карло — тысячи статистических экспериментов. Расчёты делают в программах Excel или Python. Для этого нужно знать специальные формулы и коды. Чем больше прогонов, тем точнее вероятность
- Итоговые значения, которые предлагает программа, нужно проанализировать. Для этого можно построить график кумулятивного распределения, используя ИИ




















